Chris Verhoek -- Research

Our paper "Fundamental Lemma for Data-Driven Analysis of Linear Parameter-Varying Systems" (you can find the preprint here) has been accepted for the 60th IEEE Conference on Decision and Control!
In this post, we want to add some extra information regarding the final prediction example in terms of simulation data. Moreover, we add another example with a random static, affine LPV-IO system^[1]. We first give additional figures regarding the example in the paper, then we will give the additional example. The additional example can also be found on the APROCS website (https://aprocs.eu).

Example in CDC paper

In this example, we use the system given below.

--- Data-dictionary: Input data ---

--- Data-dictionary: Scheduling data ---

--- Data-dictionary: Output data ---

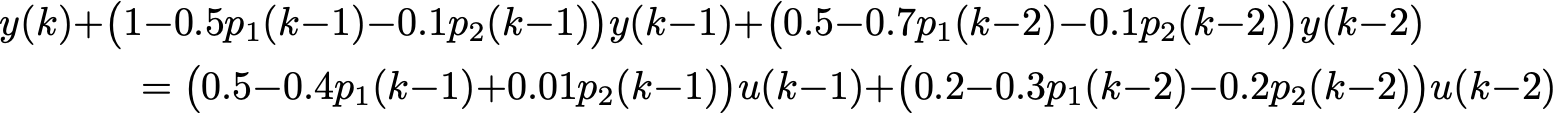
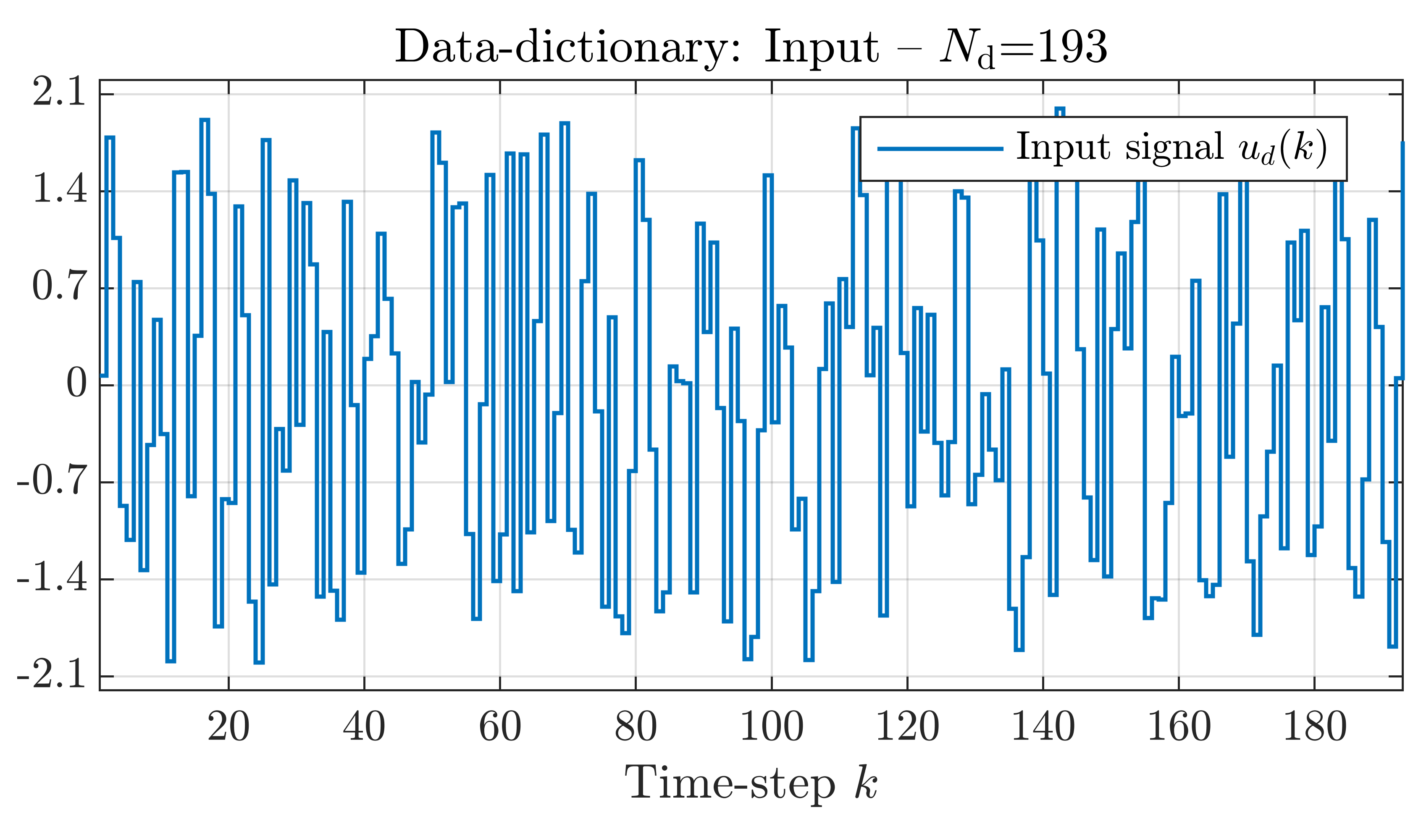
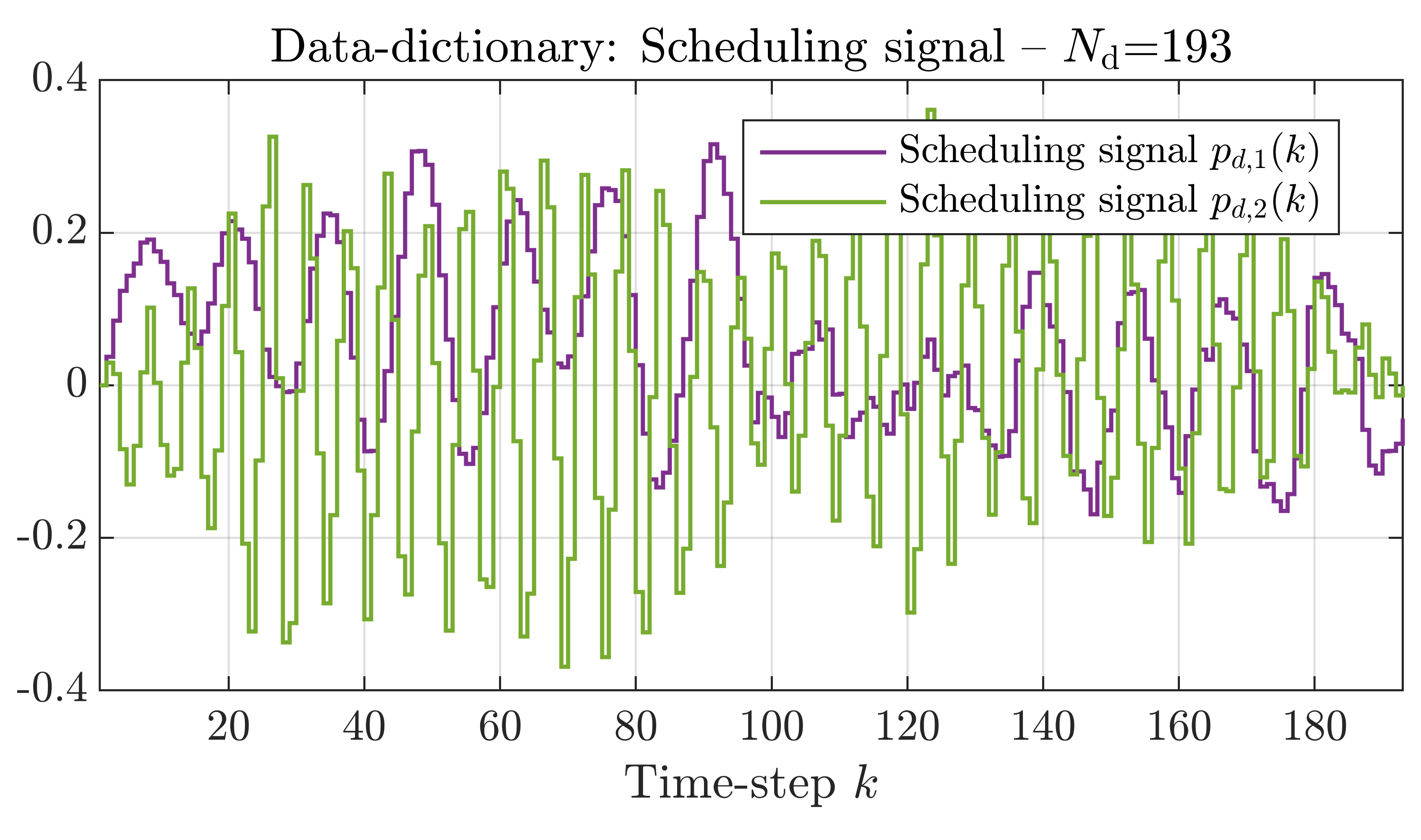
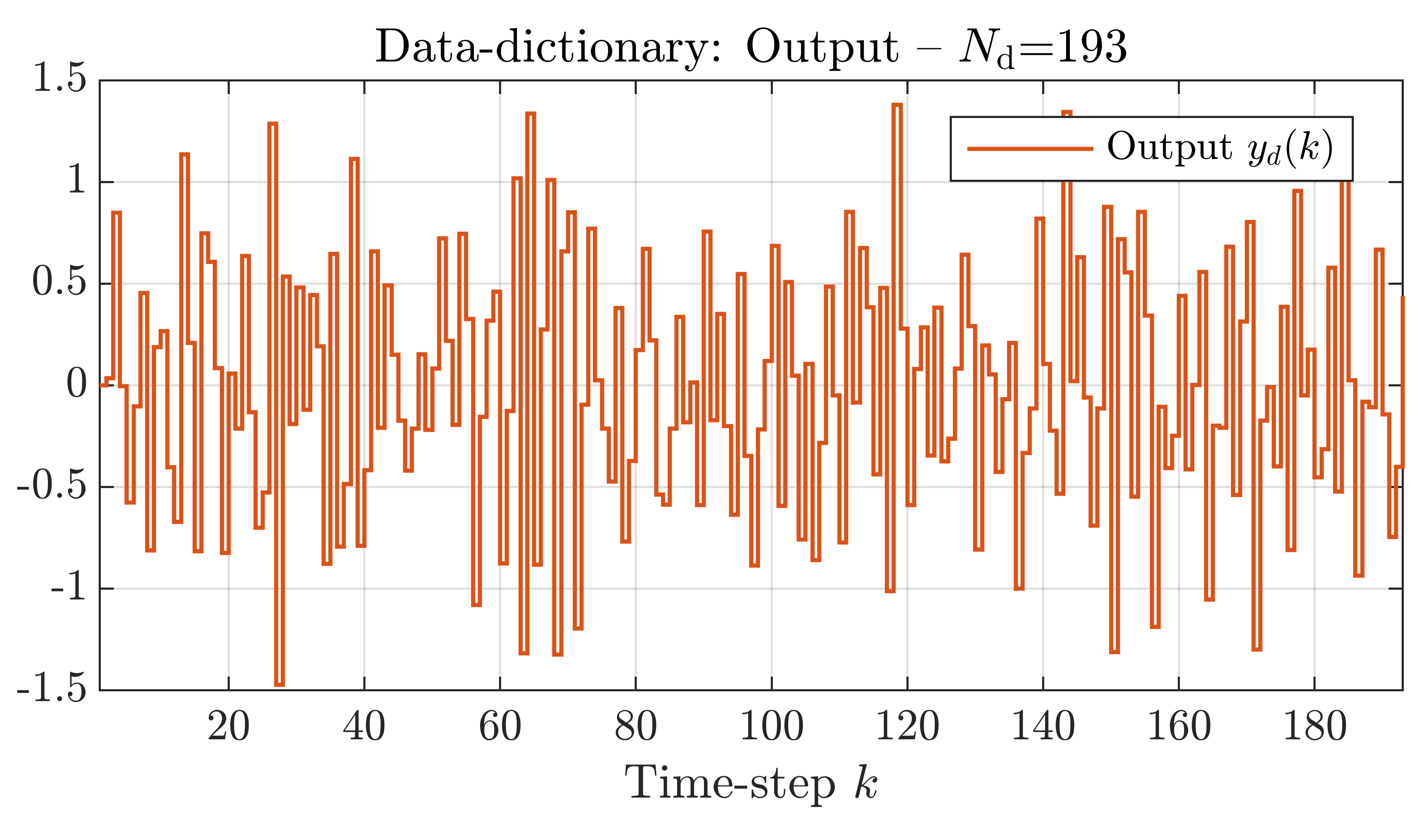
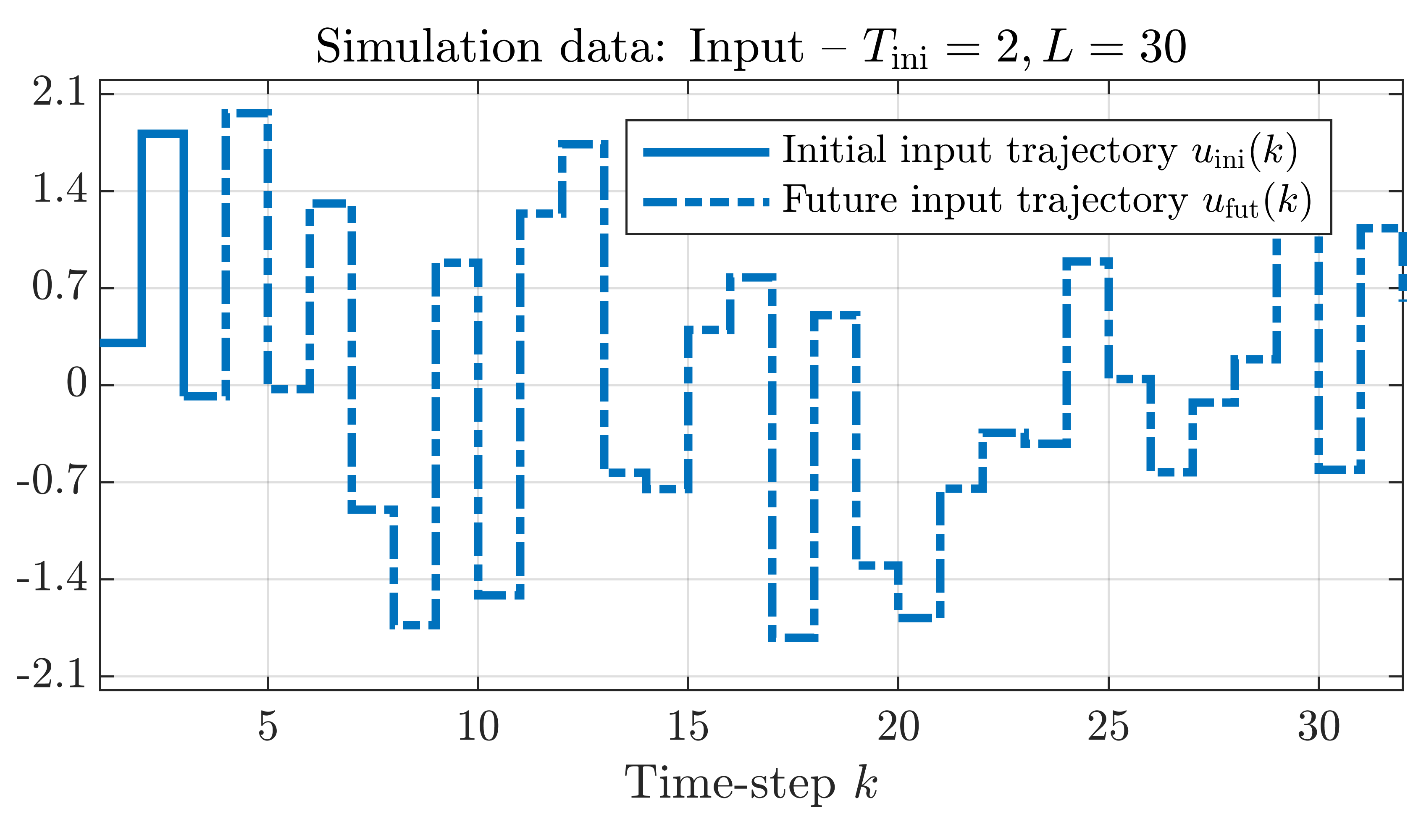
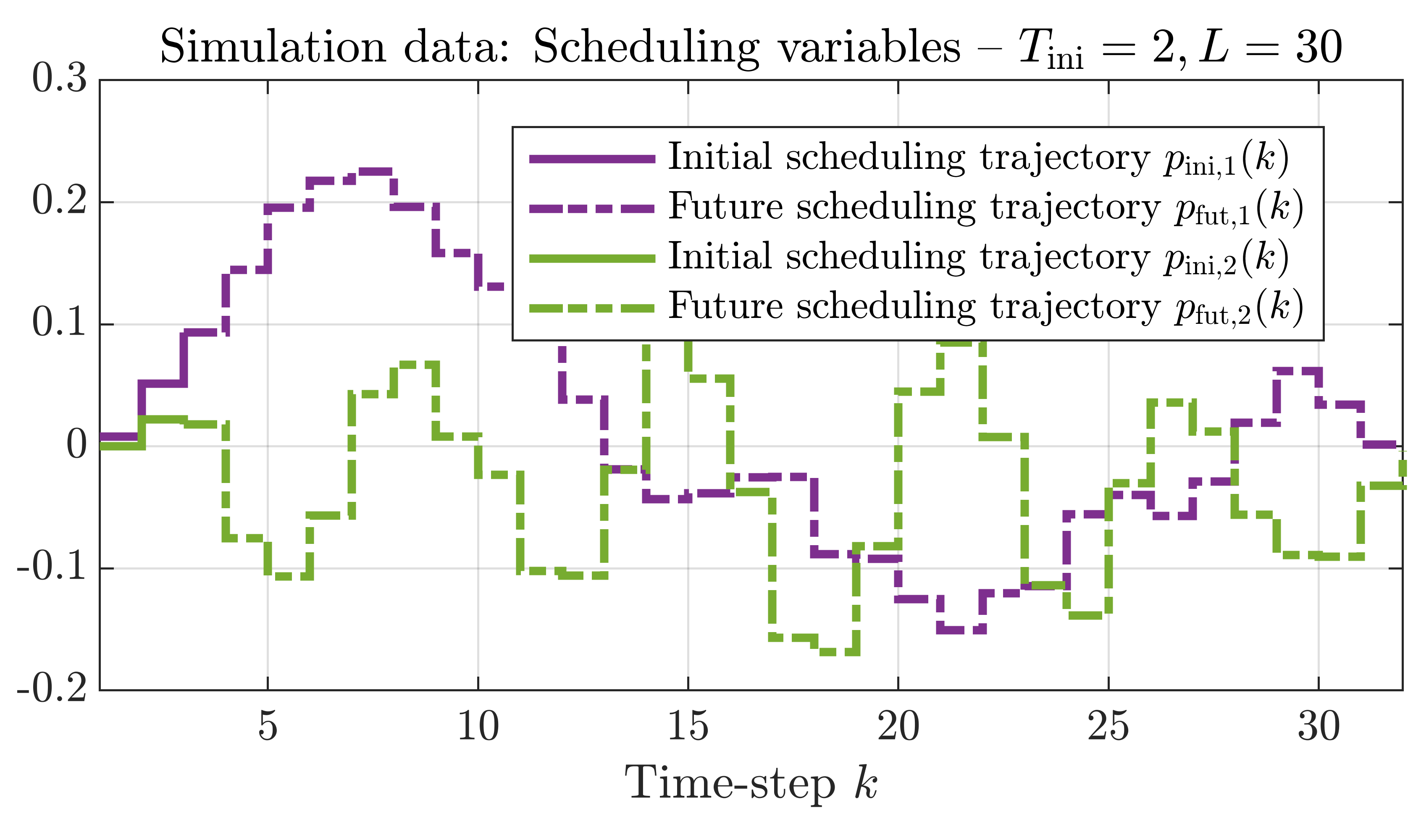
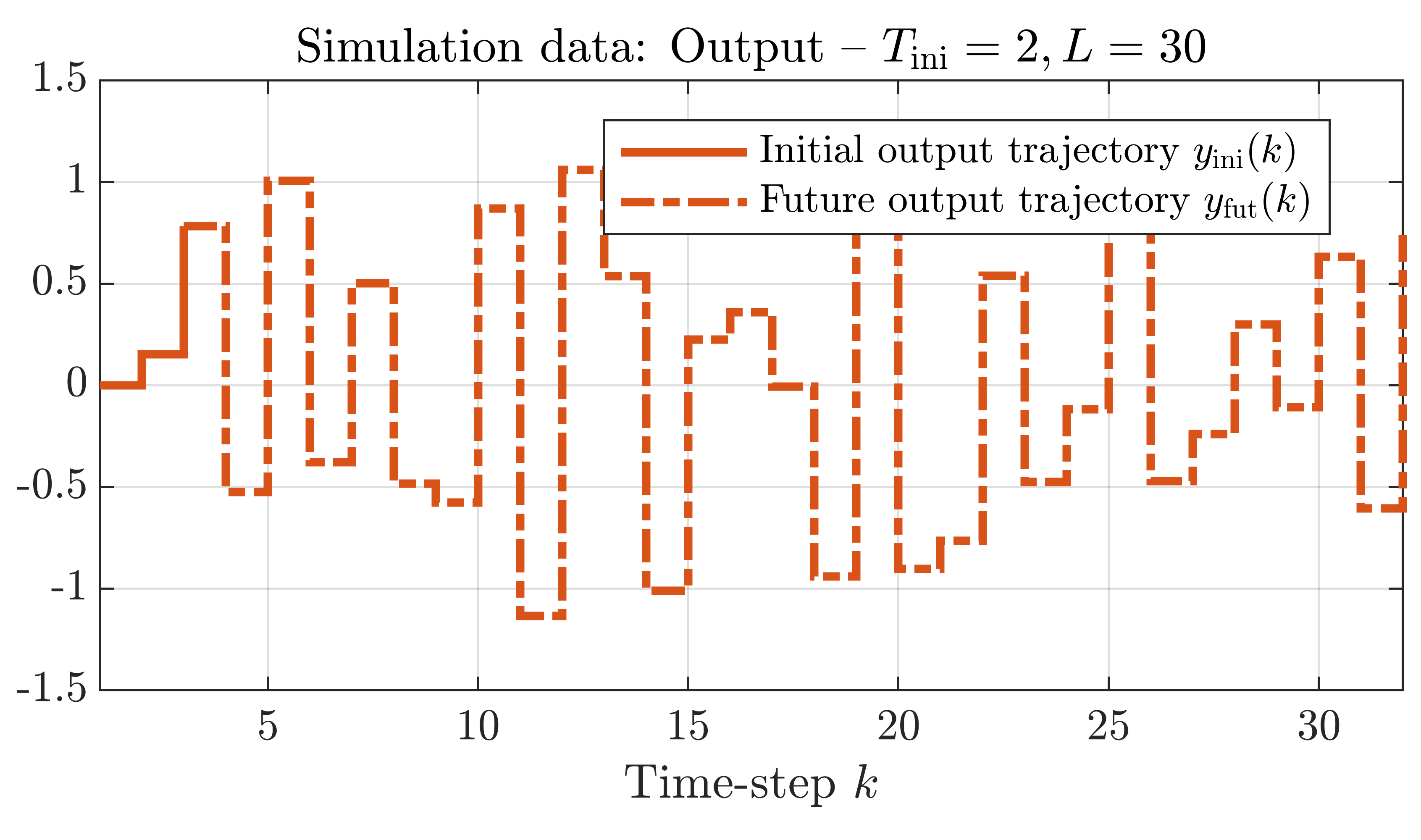
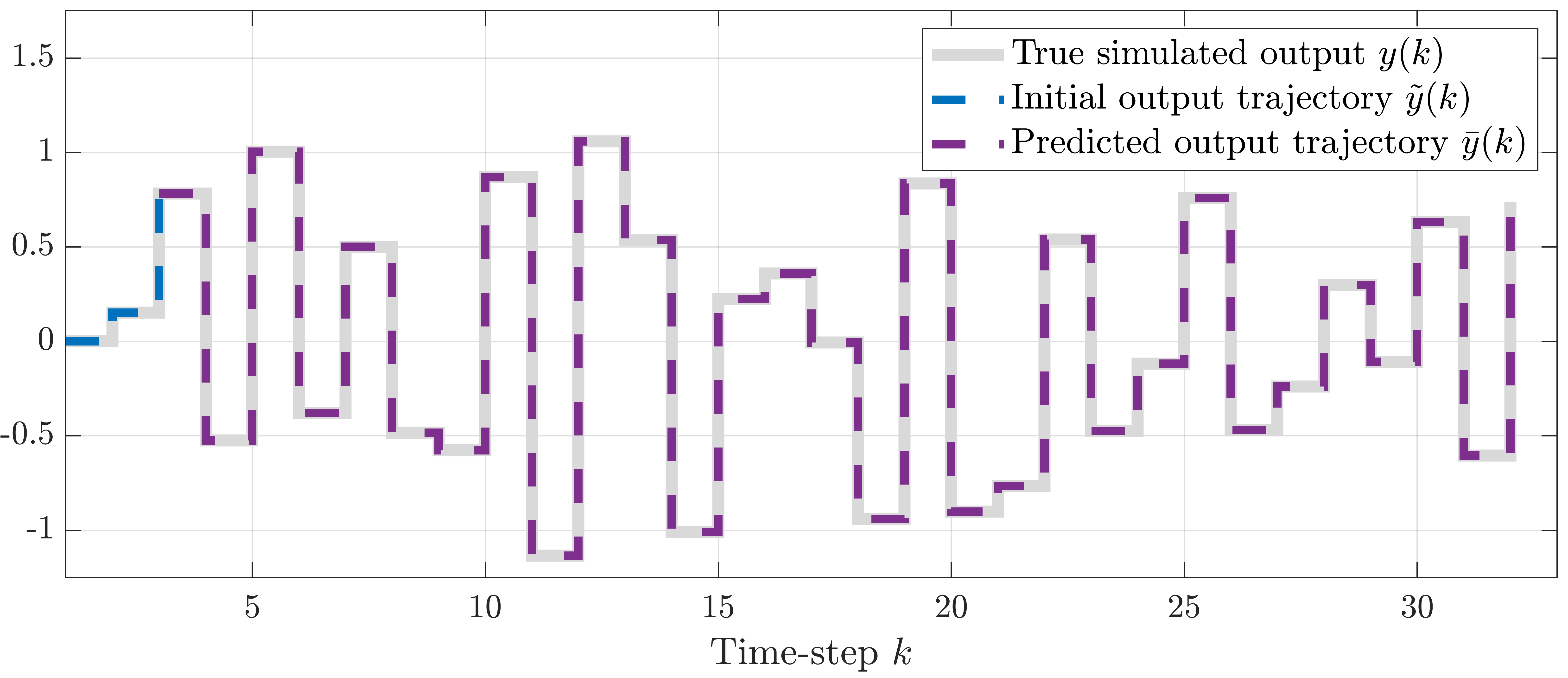
In order to build up our simulation problem, we use the paper by Markovsky and Rapisarda [2]. See for more details our LPVS or CDC papers. We simulated an additional trajectory of length L + T_ini, where L = 30 is the length of the prediction and T_ini = 2 the length of the initial trajectory. In the simulation problem, the initial input, output and scheduling trajectories incorporate the initial conditions into the problem and ensure that the predicted output continues smoothly after the Tini'th time-step. In order to accurately predict the length L output, the associated inputs and scheduling signals are also incorporated into the problem. Hence, the future inputs and scheduling signals are assumed to be known. The simulation data we used in the example are shown in the plots below (click on the plots to enlarge), note that the output trajectory is only used to compare the prediction with the true output trajectory.

--- Simulation data: Input ---

--- Simulation data: Scheduling ---

--- Simulation data: Output ---

Using this data, the future output is predicted and compared to the simulated output shown above. The result is shown below, which is the same plot as in the CDC paper.

Additional MIMO example

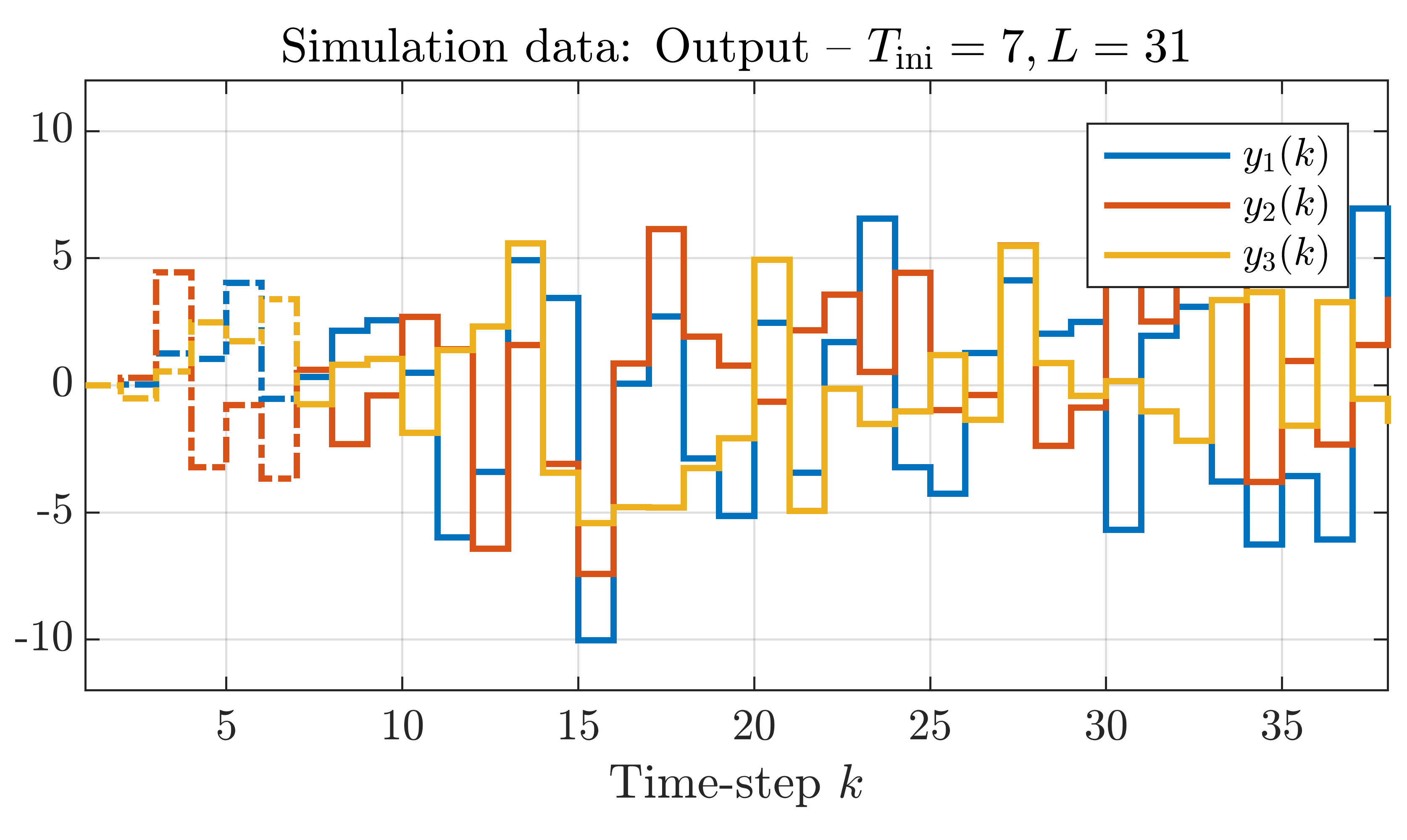
In this example, we again have a simulation problem, but now for a random, static-affine MIMO LPV system, i.e.,

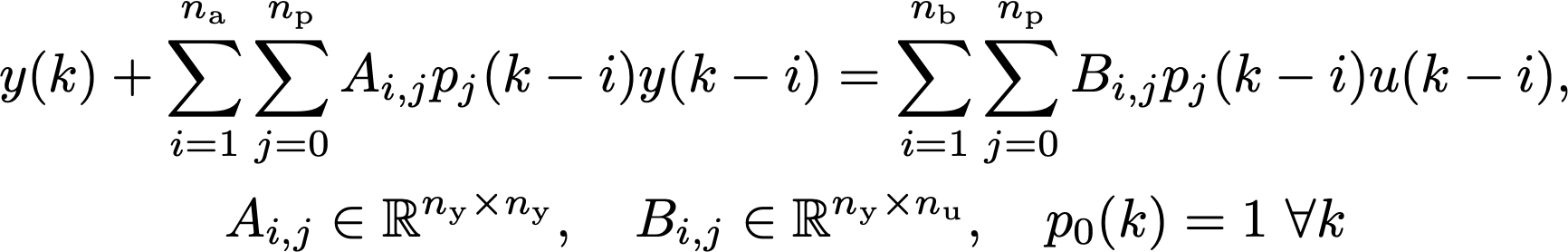
n_u = 2, n_p = 4, n_y = 3, n_a = 7, n_b = 6, T_ini = 7, L = 31, N_d = 894

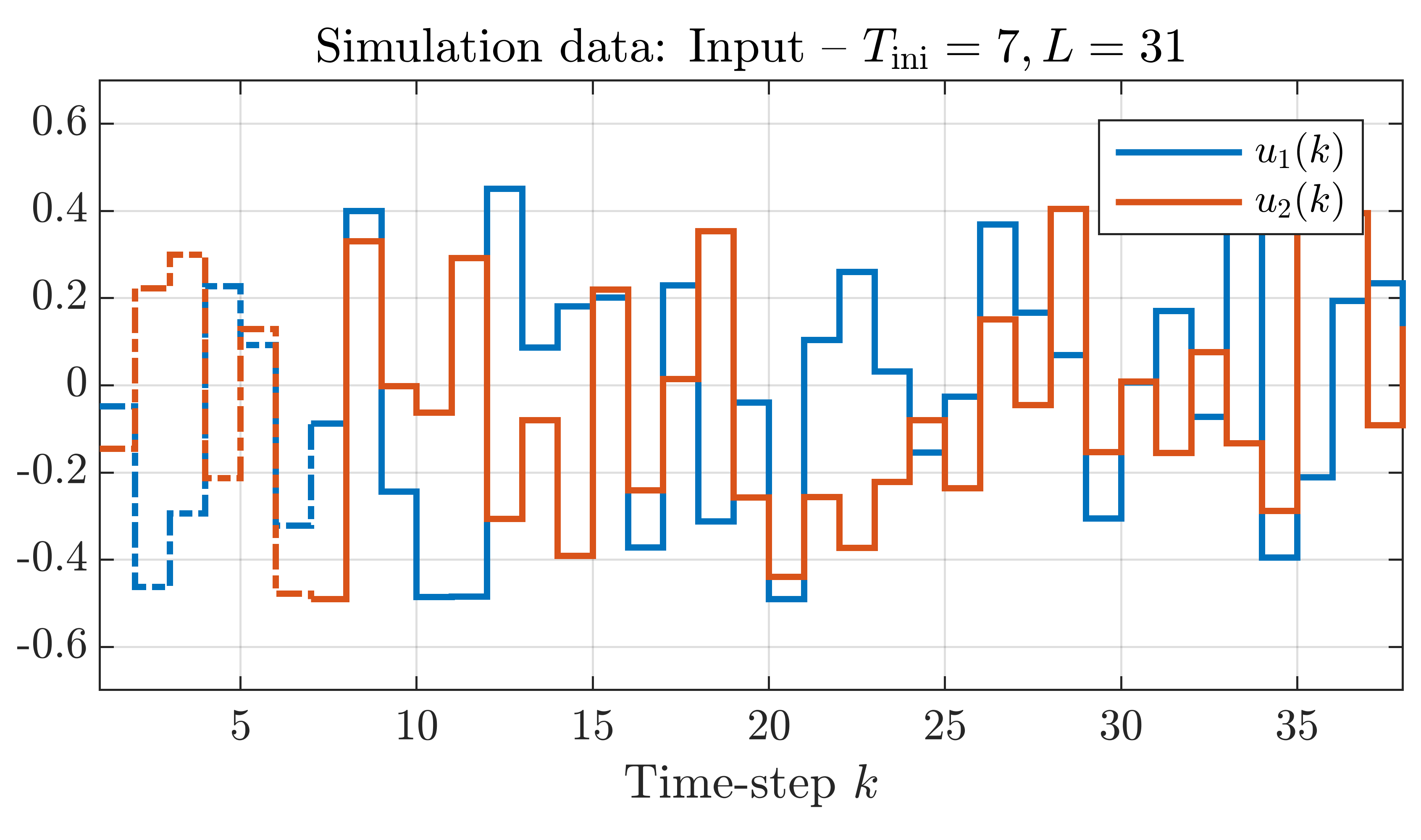
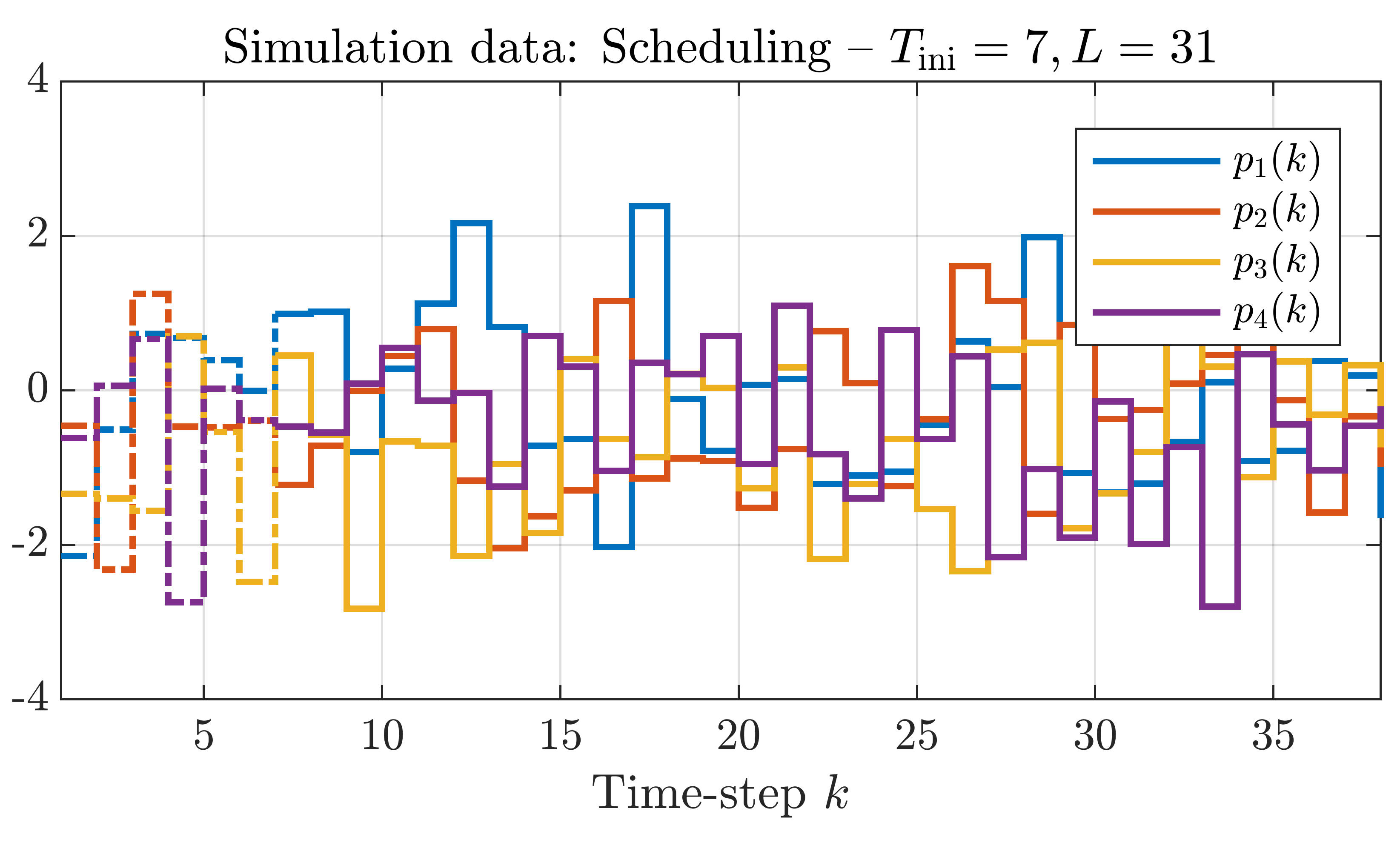
The data dictionary is generated using random input and scheduling sequences. We will not show the data dictionary due to the large number of data points. We perform the prediction using the simulation data shown in the plots below (again, click on the plots to enlarge).

--- Simulation data for random MIMO LPV system: Input ---

--- Simulation data for random MIMO LPV system: Scheduling ---

--- Simulation data for random MIMO LPV system: Output ---

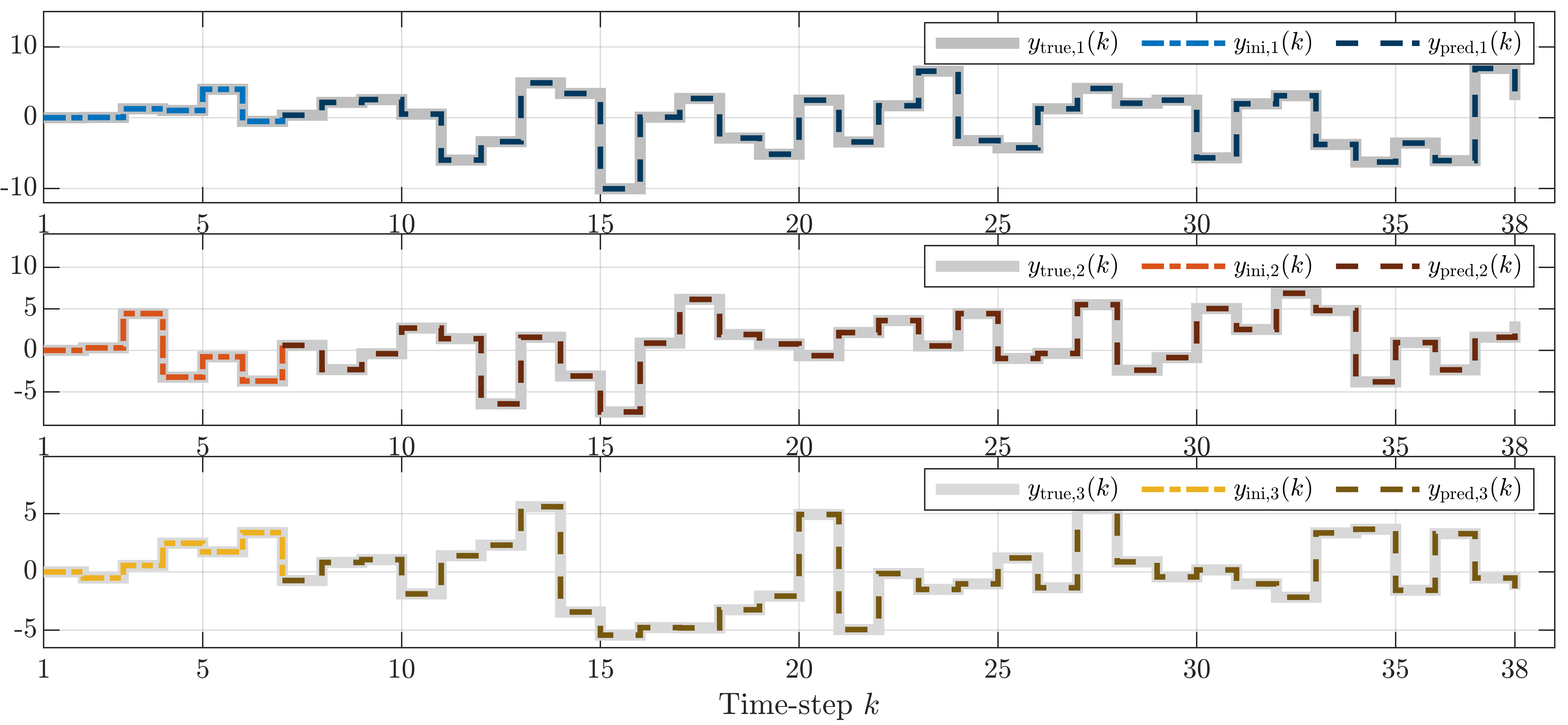
Using this data, the future output sequence is predicted and compared to the simulated output sequence shown in the above-right plot. Again, the data-dictionary does exactly represent the system, as all the outputs of the MIMO LPV system are predicted perfectly. The prediction result is shown in the figures below (click on the figure to enlarge).

--- Prediction results for the MIMO system ---

The first, second and third plot correspond to the first, second and third output, respectively. In the plots, the gray line is the baseline output from the simulation data. The dash-dotted line is the initial trajectory that is used in the simulation problem to account for the initial condition while the dashed, darker colored line is the prediction of the n^th output. The error between the baseline and the predicted output in the order of numerical accuracy.

1. [1]: We might add an example with a different dependency in the future.
2. [2]: I. Markovsky and P. Rapisarda,"Data-Driven Simulation and Control," International Journal of Control, vol. 81, no. 12, p. 1946-1959, 2008.

Back to top